The Quantum Fractal Connection: Unifying Spacetime, Energy, and Dimensions

Quantum mechanics introduced a revolutionary principle: that energy and momentum are not continuous but quantized, existing in discrete packets or “quanta.” This idea fundamentally shifted our understanding of the universe, emphasizing a granular, stepwise nature to processes previously thought to be smooth. At the same time, fractals—geometric structures characterized by self-similarity and fractional dimensions—have provided tools for understanding complex, irregular systems in nature. Despite their apparent differences, quantum mechanics and fractal geometry may share an underlying connection: the idea of discreteness.

Fractal dimensions, such as the Hausdorff dimension, are typically treated as continuous in mathematical theory. Yet, real-world fractals often exhibit discrete scaling behaviors, suggesting a potential quantization of dimensionality. This paper proposes that fractal dimensions themselves may be discrete, forming the foundational structure of spacetime and linking quantum mechanics to string theory.

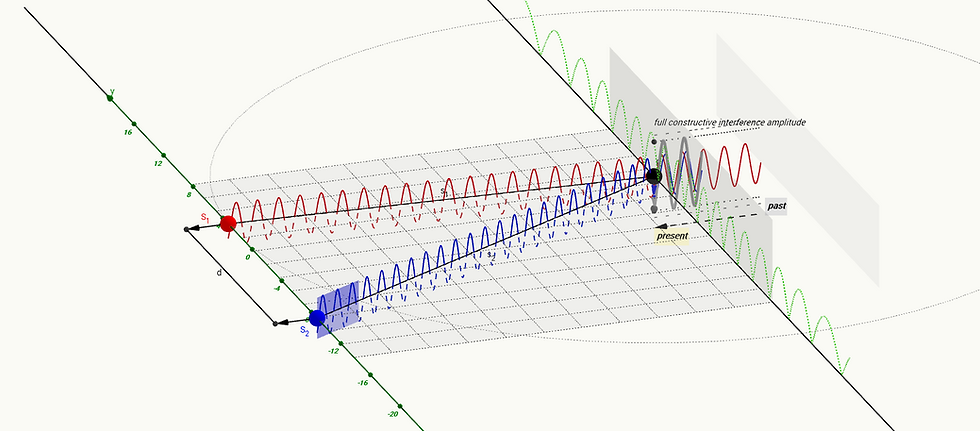
In string theory, particles arise from the vibrations of one-dimensional strings in compactified extra dimensions. If these extra dimensions are fractal and quantized, it may explain why particles and fields emerge in discrete states, connecting the geometry of spacetime to the behavior of energy and matter. This hypothesis offers a pathway to unify quantum mechanics, fractal geometry, and string theory into a cohesive framework.

2. Mathematical Framework

2.1. Fractal Dimensions

Fractal dimensions describe structures that do not fit neatly into integer dimensions. For example, a line is one-dimensional, and a square is two-dimensional. But fractals like the Koch snowflake or the Sierpinski triangle occupy fractional dimensions, which are defined mathematically by their scaling properties.

The Hausdorff dimension (dh) is given by:

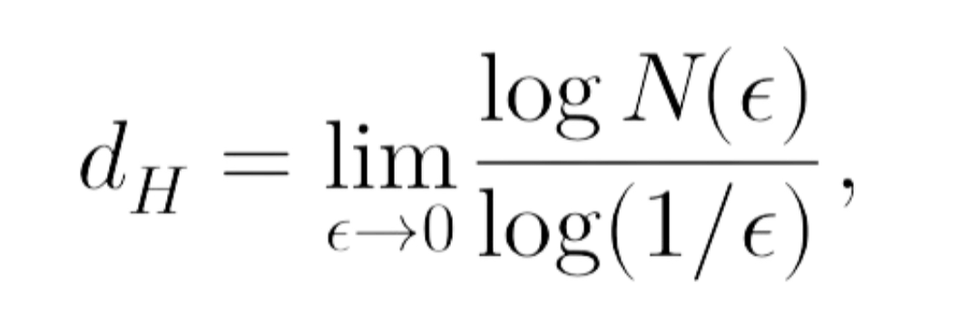
Where

is the number of self-similar pieces of size

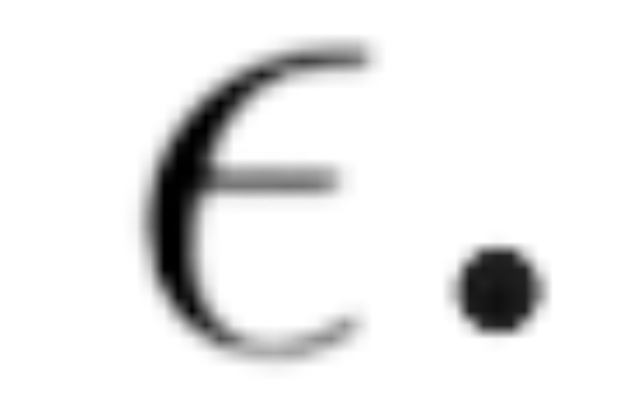
For example, the Koch curve has

approximately 1.26.

In a quantized framework,

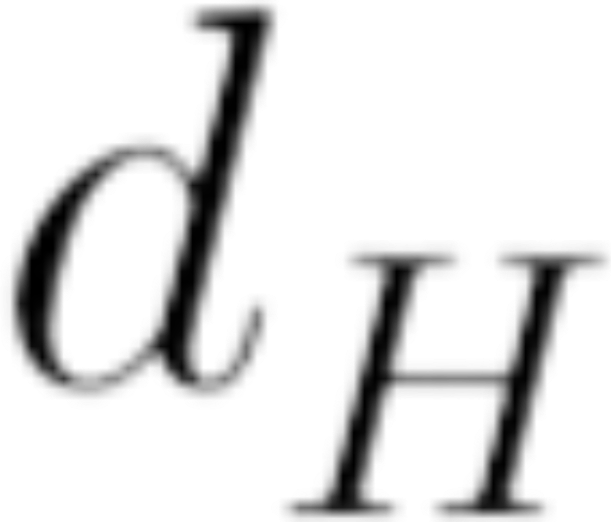
would take on discrete values:

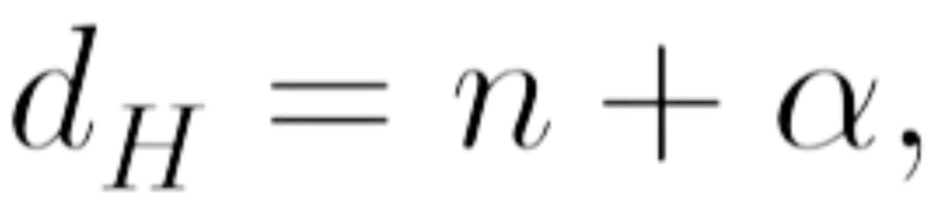
where n is an integer and a is a fractional constant representing the scaling limit of each fractal state.

2.2. Quantum Mechanics

In quantum mechanics, physical quantities like energy and angular momentum exist in discrete states. The energy of a photon is quantized as:

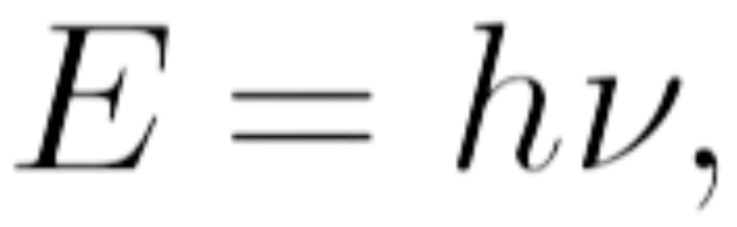
where h is Planck’s constant and  is the frequency of the photon.

Similarly, the angular momentum of an electron in an atomic orbit is quantized in units of , Planck’s constant divided by:

If fractal dimensions are quantized, the relationship between energy and dimensionality could be expressed as:

implying that higher fractal dimensions correspond to lower energy states, just as electrons in higher atomic orbits have lower binding energies.

2.3. String Theory

String theory suggests that the fundamental constituents of matter are not point particles but vibrating strings. These strings interact within higher-dimensional spaces, which are compactified into shapes like Calabi-Yau manifolds. The vibrational modes of these strings determine the properties of particles, such as mass, charge, and spin.

If these compactified dimensions are fractal and quantized, the vibrational modes of strings would also be constrained by the discrete fractal structure. This could lead to new predictions about particle spectra:

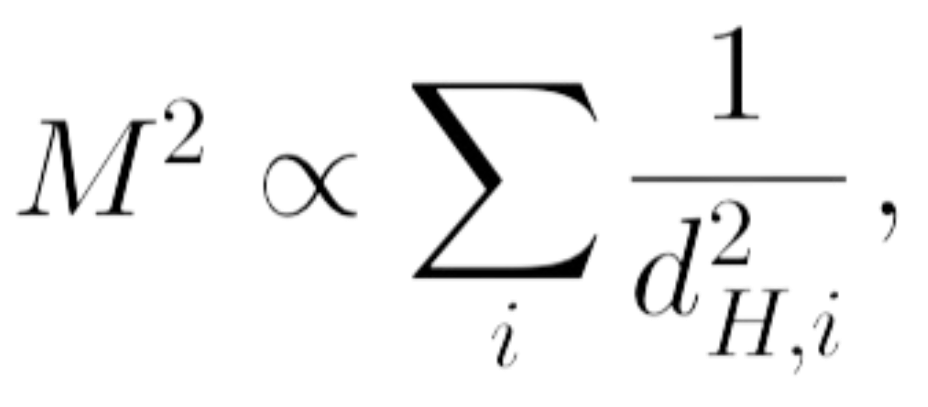
where  dH, i represents the discrete fractal dimensions of the compactified space.

3. Compatibility with Existing Theories

3.1. Quantum Mechanics

Quantized fractal dimensions align with the discrete nature of quantum mechanics, extending the concept of quantization from energy levels to the structure of spacetime itself. This builds on the concept of “quantum foam,” proposed by Wheeler (1957), which suggests that spacetime at the smallest scales is not smooth but highly irregular and discrete.

3.2. Fractal Geometry

Fractals have long been used to model systems in nature, from the branching patterns of trees to the distribution of galaxies. Mandelbrot (1982) observed that real-world fractals often exhibit discrete scaling behaviors, which may reflect an underlying quantization of dimensionality.

3.3. String Theory

String theory’s reliance on higher-dimensional spaces provides a natural context for exploring fractal dimensions. The compactified dimensions of string theory are often assumed to be smooth, but introducing discrete fractal structures could refine our understanding of how particles and fields emerge.

4. Testable Predictions

4.1. Fractal Scaling in Quantum Fields

Quantum fields, such as the electromagnetic or Higgs field, may exhibit fractal-like scaling properties under certain conditions. For example, high-energy collisions in particle accelerators might reveal patterns consistent with discrete fractal dimensions.

4.2. Discrete Dimensional Transitions

If dimensions are quantized, transitions between discrete fractal dimensions could produce unique particle signatures. These might include unexpected mass-energy distributions or deviations from standard quantum predictions.

4.3. Cosmological Observations

Cosmological phenomena, such as the cosmic microwave background (CMB), may contain fractal patterns that reflect the discrete structure of spacetime. Anisotropies in the CMB could provide clues to the fractal nature of the universe.

5. Discussion

The hypothesis of discrete fractal dimensions offers a unifying framework for understanding the intersection of quantum mechanics, fractal geometry, and string theory. It suggests that the discreteness observed in quantum mechanics may extend to the very fabric of spacetime, with fractals providing a natural mathematical framework for modeling this structure.

This framework has implications for multiple fields, from particle physics to cosmology. By quantizing fractal dimensions, we may gain new insights into the origins of particles, the behavior of fields, and the geometry of the universe itself.

6. Conclusion

The quantization of energy is a cornerstone of quantum mechanics, and fractals provide a powerful tool for modeling complex systems. By combining these ideas, this paper proposes a new hypothesis: that fractal dimensions are discrete, forming the foundation of quantum mechanics and string theory. This framework invites further exploration, offering testable predictions and a pathway to unify disparate areas of physics.

Works Cited

    •    Mandelbrot, B. (1982). The Fractal Geometry of Nature. W. H. Freeman and Co.

    •    Polchinski, J. (1998). String Theory, Vol. 1: An Introduction to the Bosonic String. Cambridge University Press.

    •    Wheeler, J. A. (1957). “On the Nature of Quantum Geometrodynamics.” Annals of Physics, 2, 604–614.

    •    Heisenberg, W. (1927). “Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik.” Zeitschrift für Physik, 43, 172-198.