The Importance of Visualizing Mathematics: Insights from Visionaries
- professormattw
- Jan 19
- 4 min read
"Pure mathematics is, in its way, the poetry of logical ideas." These words from Albert Einstein encapsulate the beauty of mathematics—a subject often misunderstood as a collection of abstract symbols devoid of tangible meaning. However, when we delve into the works of great thinkers such as Einstein, Niels Bohr, Max Born, and J. Robert Oppenheimer, a common thread emerges: the essential role of visualization in understanding and applying mathematical concepts. In this blog post, we explore how visualizing mathematics transforms equations into meaningful representations and why this approach is essential for effective education, particularly in foundational and advanced mathematical concepts.

Algebra as Visual Sheet Music
Algebra is frequently taught as a purely symbolic manipulation of variables and equations, leading many students to view it as an abstract, unapproachable discipline. Yet, the visual nature of algebra is fundamental. Consider an equation as a piece of sheet music: the notes correspond to sound, and the algebraic symbols correspond to geometric and visual structures. For instance, a linear equation represents a line, while a quadratic equation corresponds to a parabola. Ellipses, circles, and hyperbolas are brought to life by conic sections—geometric shapes derived from slicing a cone at various angles. To grasp algebra deeply, students must visualize these structures, much like musicians internalize the auditory patterns represented by notes.
A pioneering advocate of this approach, physicist Max Born, emphasized the interplay between algebra and geometry in his foundational work on quantum mechanics. He argued that mathematical symbols are not mere abstractions but bridges to physical reality. Educators must teach algebra not just as a tool for solving equations but as a medium for visualizing and conceptualizing relationships in space.
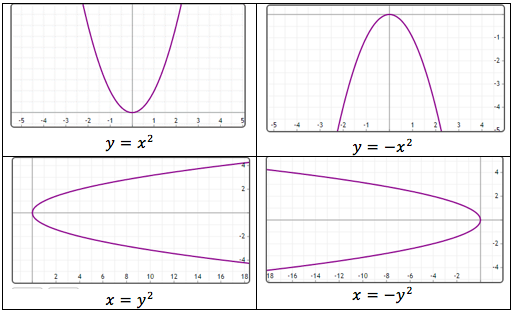
Geometry and Trigonometry: Foundations for Algebra
While algebra is often introduced first in traditional curricula, a strong case can be made for grounding students in geometry and trigonometry before advancing to algebra. Geometry inherently cultivates spatial reasoning and visual thinking, laying a natural foundation for algebraic concepts. For example, understanding the relationship between the slope of a line and the tangent of an angle in trigonometry provides an intuitive pathway to grasping derivatives in calculus.
Trigonometry, with its focus on angles, triangles, and periodic functions, is a cornerstone for visualizing algebraic and calculus concepts. The sine and cosine functions, represented as oscillatory waveforms, exemplify how mathematical symbols correspond to real-world phenomena such as sound waves and light patterns. By embedding trigonometric visualization in early education, we can demystify more advanced topics such as Fourier analysis and wave mechanics.
Derivation and Integration: Separate Visual Paradigms
Calculus is often treated as a monolithic subject, with differentiation and integration grouped together under a single banner. However, these concepts demand distinct visual interpretations:
Derivation is fundamentally about visualizing slope and change. The derivative of a function corresponds to the tangent line at a point, illustrating instantaneous rate of change. This geometric interpretation aligns naturally with the concepts introduced in algebra.
Integration, on the other hand, is a geometric tool for understanding area under a curve. It is inherently connected to the principles of geometry and trigonometry, as the integral often represents accumulation or totality in a spatial context.
To optimize educational outcomes, derivation should be integrated into algebra instruction, emphasizing its relationship to rates of change and slope. Conversely, integration should be introduced alongside geometry and trigonometry, leveraging its spatial and accumulative properties. By aligning these concepts with their natural visual frameworks, we empower students to see the connections between mathematics and the physical world.
Visualizing Number Theory and Statistics
Number theory and statistics are often regarded as highly abstract disciplines. However, their true power lies in their visual representations:
Number theory gains clarity through graphical representations such as modular arithmetic diagrams, prime number spirals, and geometric interpretations of congruences.
Statistics becomes accessible when data is visualized through histograms, scatter plots, and probability distributions. These visual tools make abstract concepts like variance, correlation, and standard deviation tangible and comprehensible.
Until students can visualize the meaning behind mathematical symbols and equations, their understanding remains superficial. As Max Born suggested, “Mathematical symbols are shorthand devices to represent physical realities.” In education, we must prioritize tools and techniques that bring these realities to life.
Physics and Higher Mathematics: The Need for Visualization
The relationship between mathematics and physics underscores the importance of visualization. Einstein’s theory of relativity, for example, relied heavily on his ability to visualize concepts like spacetime curvature. Similarly, Niels Bohr’s model of the atom was a direct product of visualizing quantum phenomena.
Unfortunately, traditional education often neglects this aspect, reducing mathematics to rote memorization and procedural drills. This approach fails to prepare students for higher concepts in physics and engineering, where visualization is not just helpful but essential. For instance, Maxwell’s equations, which describe electromagnetic fields, are best understood through visual representations of field lines and wave propagation. By integrating visual learning tools such as simulations, diagrams, and interactive models, we can bridge this gap and equip students with the skills needed for advanced study.

Conclusion: A Call to Visualize
Mathematics is not a collection of abstract symbols; it is a language that describes the universe in visual and tangible ways. As educators, we must emphasize the visual nature of mathematics at every level of instruction. From algebra as sheet music to the geometric underpinnings of calculus, from the visual tools of statistics to the graphical insights of physics, visualization transforms abstract concepts into meaningful understanding.
By fostering this approach, we honor the insights of visionaries like Einstein, Bohr, Born, and Oppenheimer. More importantly, we equip the next generation with the tools they need to not only understand mathematics but to see the world through its elegant lens.
Works Cited
Einstein, Albert. Relativity: The Special and General Theory.
Born, Max. Natural Philosophy of Cause and Chance.
Bohr, Niels. Atomic Physics and Human Knowledge.
Oppenheimer, J. Robert. Science and the Common Understanding.
Stewart, Ian. Concepts of Modern Mathematics.
Penrose, Roger. The Road to Reality: A Complete Guide to the Laws of the Universe.










Comments