Negative Time in Quantum Physics: Paradoxes, Positrons, and Time-Symmetric Interpretations.

Introduction:

Time is usually assumed to flow in one direction from past to future, but quantum physics sometimes permits descriptions that challenge this intuition. The concept of “negative time” – essentially processes unfolding backward in time – is highly counterintuitive and even paradoxical from a classical standpoint, as it conjures images of effects preceding their causes. In quantum mechanics, however, certain formalisms and interpretations suggest that under the right circumstances, the mathematics allows time-symmetric or even retrocausal descriptions. For example, recent experiments have reported phenomena where particles appear to “exit” an interaction before entering it, implying a negative time delay . While such results do not represent macroscopic time travel, they underscore that quantum processes can defy our usual temporal ordering. These observations motivate an in-depth exploration of how negative time can be understood within quantum physics. In this report, we examine the paradoxical nature of negative time and how it fits within quantum mechanics, the idea (originating with Feynman and Stueckelberg) that antiparticles like positrons can be viewed as electrons moving backward in time, and the use of Feynman diagrams to represent interactions in a time-reversible framework. We then discuss retrocausality and time-symmetric interpretations of quantum mechanics, including the Wheeler–Feynman absorber theory and Cramer’s transactional interpretation, and consider experimental and theoretical implications of time-reversal symmetry. Throughout, we confront the apparent paradoxes of negative time and clarify how quantum theory manages to remain consistent with causality and observed physical laws.

Negative Time in Quantum Mechanics: Paradox and Framework

Classical physics is built on causal dynamics: a cause at an earlier time t produces an effect at a later time t+Δt. Allowing negative time (or backward-in-time influence) in a classical context leads to logical paradoxes like the infamous “grandfather paradox.” In quantum mechanics, the situation is more subtle. The fundamental equations of motion (such as the Schrödinger equation or Dirac equation) are largely time-symmetric – if one reverses the direction of time evolution (and, for some systems, takes a complex conjugate of the wavefunction), the equations remain valid. This time-reversal symmetry means that for any allowed quantum process, a time-reversed process is also formally allowed by the equations of motion. Indeed, quantum theory “provides a framework” with enormous predictive success, yet there is debate on what underlying reality it implies . Some interpretations even hypothesize backward-in-time causal influences, or retrocausality, to explain quantum phenomena . On the face of it, such backward-time influences seem paradoxical, threatening causality. However, quantum mechanics has mechanisms that prevent true causal paradoxes. Notably, even time-symmetric quantum interpretations enforce consistency via the so-called “no-signaling” constraints – an observer cannot send information to the past and create a contradiction. In essence, negative time in quantum mechanics typically emerges in a mathematical or interpretational sense rather than as literal reversals of macroscopic time flow. For example, the puzzling negative delays observed in certain quantum optical experiments are explained by the distortion of wave packets and the quantum uncertainty principle, not by photons literally traveling into the past . The measurement process in quantum mechanics, on the other hand, is not time-symmetric: once a measurement occurs, the wavefunction “collapses” (in the Copenhagen view) irreversibly, introducing a preferred direction of time associated with thermodynamic irreversibility and information gain. This dichotomy – time-symmetric dynamics vs. time-asymmetric measurements – is at the heart of the quantum arrow of time. It suggests that negative-time formalisms must be applied with care to avoid conflict with the observed arrow of time. In summary, the notion of negative time highlights profound questions about time’s role in quantum theory, but within the standard framework these questions are answered in ways that preserve overall consistency. Physicists reconcile the formal possibility of processes “running backward” with the practical impossibility of undoing quantum measurements or sending signals to one’s own past. As we will see, allowing negative time in quantum descriptions can be fruitful and paradox-free if interpreted properly, especially when discussing antiparticles and time-symmetric formulations of quantum theory (Aharonov & Vaidman, 2007; Price, 1997) .

Positrons as Electrons Moving Backward in Time (Feynman–Stueckelberg Interpretation)

One of the most striking instances of “negative time” in physics is the interpretation of antiparticles. The idea originated in the 1940s from work by Ernst Stueckelberg and, independently, Richard Feynman. Stueckelberg (1942) proposed that the positron – the antiparticle of the electron – could be viewed as an electron moving backward in time with positive energy . This was a radical reinterpretation of the negative-energy solutions that had appeared in Paul Dirac’s relativistic wave equation. In Dirac’s original picture, negative-energy electron states were reinterpreted as a “sea” of filled states, and a vacancy in this sea would behave like a positively charged electron (a positron) moving forward in time (Dirac, 1930). Stueckelberg’s alternative was to dispense with the hole metaphor and literally consider the mathematical solution as an electron whose worldline is reversed in time. A few years later, Feynman adopted this idea and integrated it into the emerging framework of quantum electrodynamics (QED). In his 1949 paper “The Theory of Positrons”, Feynman showed that one can equivalently view a positron traveling forward in time as an electron traveling backward in time in spacetime diagrams . As Feynman put it, “the ‘negative energy states’ appear…as waves traveling…backwards in time. Experimentally, such a wave corresponds to a positron” . In other words, instead of treating positrons as an entirely new kind of particle, one can treat them as electrons propagating backward through time. This interpretation elegantly explained why positrons have the same mass and spin as electrons but opposite charge: reversing the time direction flips the charge sign in the mathematical formalism (related to an operation called charge conjugation combined with time reversal) .

An illustrative (if fanciful) consequence of Feynman’s insight was conveyed to him by his mentor John Wheeler. Wheeler suggested that perhaps all electrons in the universe are actually one and the same electron zig-zagging through time, reappearing as a positron whenever it reverses direction . This one-electron universe idea was more of a thought-provoking anecdote than a serious theory – among other issues, it would imply equal numbers of electrons and positrons in the universe, contrary to observation – but it dramatizes the implication of Feynman’s picture that particle-antiparticle pairs could be two aspects of a single entity’s worldline. In practice, what Feynman and Wheeler found is that this interpretation greatly simplifies the calculation of particle interactions. It allowed them to use the same machinery for an electron scattering forward in time as for a positron scattering backward, unifying the treatment of particles and antiparticles. Anderson’s experimental discovery of the positron in 1932 (Anderson, 1933) lent credence to the Dirac/Stueckelberg/Feynman picture by confirming that “negative-energy electrons” manifest as real antiparticles.

It is important to clarify that when physicists say “a positron is an electron moving backward in time,” they are speaking in the context of a relativistic space-time diagram or mathematical formalism, not literally asserting that positrons arrive before they depart. In a modern quantum field theory, this phrase is a shorthand for the fact that the propagation of an antiparticle with positive energy forward in time is mathematically equivalent to the propagation of a particle with negative energy backward in time . For example, the negative-energy solutions of the Dirac equation can be reinterpreted through a change of variables as positive-energy solutions traveling backward in time . This equivalence is sometimes called the Feynman–Stueckelberg interpretation. In plain terms, an antiparticle can be treated as a particle going from the future to the past. This interpretation is embedded in the very architecture of quantum electrodynamics and has been experimentally validated by the success of QED in predicting results involving positrons (Feynman, 1949; Dyson, 1949). Notably, Feynman warned against over-interpreting this imagery: we cannot use a positron to communicate with the past or resurrect bygone events. The backward-in-time language works at the level of interactions and amplitudes, but an isolated positron in our laboratory still appears to move forward in our time. In fact, when a positron is observed, it annihilates with an electron and produces photons – an event that, viewed in reverse, looks like pair creation. In Feynman’s picture, that annihilation can be seen as the electron worldline turning around and going back in time. Such a process is perfectly allowed in quantum field theory, but only within the constraints of the theory (e.g. energy-momentum conservation and causality of signals). Thus, no violations of causality occur: an electron-positron annihilation viewed as a single electron’s U-turn in time is still an interaction that respects all physical conservation laws and locality requirements in the lab frame .

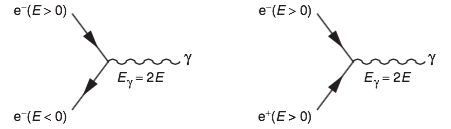
The Feynman–Stueckelberg interpretation beautifully resolves the paradox of negative time on the microscopic level by showing that what looks like backward time travel is just another way of describing antiparticle motion. It fits consistently into the framework of quantum mechanics and relativity. The paradoxes evaporate because an antiparticle going “backward in time” in a Feynman diagram does not allow an experimenter to send a message to their own past; it is simply a convenient description that respects all the normal rules of cause and effect when translated back to the usual picture (Curir, 1974; phinds, 2014) . In summary, a positron can be regarded as an electron moving backward in time in the mathematical sense introduced by Feynman and Stueckelberg (Feynman, 1949; Stueckelberg, 1942). This interpretation is now a standard element of quantum field theory and highlights how quantum physics can embrace negative time (for virtual processes) without true paradox. As Yoichiro Nambu quipped in 1950 regarding this picture: “Time itself loses sense as the indicator of the development of phenomena; there are particles which flow down as well as up the stream of time” . Nambu’s remark captures the radical shift in thinking: at the quantum level, time’s direction can sometimes be treated as just another dimension that particles can traverse in theory, even though our macroscopic experience remains firmly one-directional.

Antiparticles and Feynman Diagrams in a Time-Reversible Framework

The above interpretation is vividly realized in the language of Feynman diagrams, which are space-time cartoons of particle processes used pervasively in quantum field theory. In a typical Feynman diagram, the horizontal axis represents space and the vertical axis represents time (though diagrams are often drawn with time flowing from left to right as well). Particles are depicted as lines or arrows moving through these diagrams. In this representation, antiparticles are drawn as arrows pointing against the direction of time, i.e. moving backward along the time axis . This graphical convention is not just artifice; it encodes the important fact that an antiparticle propagator mathematically behaves like a particle propagator with reversed time parameter. For example, an electron line going from time t₁ to t₂ in the forward direction is equivalent to a positron line going from t₂ to t₁. Thus, Feynman diagrams make time-reversal symmetry explicit: any vertex or interaction in a diagram can be interpreted in either time direction. An electron emitting a photon and moving forward in time could equally be seen as that electron absorbing a photon while moving backward in time. This property is related to the crossing symmetry of scattering amplitudes in quantum field theory, which states that a particle crossing from the initial state to the final state (i.e. being reinterpreted as an antiparticle on the other side) yields a valid process (Schwartz, 2014). The use of diagrams helped convince physicists that negative-time descriptions are consistent. For instance, an electron–positron annihilation diagram can be viewed as an electron line that comes in, turns around via an interaction, and goes out backward in time as a positron – equivalent to two photons being produced in the forward-time picture . Either way, the calculated probability for the process is the same . The time-reversible nature of the fundamental interactions (electromagnetic, strong, and—if we ignore small CP violations—weak interactions) is built into these diagrams. In fact, apart from the weak force, all known fundamental interactions are symmetric under the combined operation of charge conjugation (C), parity inversion (P), and time reversal (T). This is guaranteed by the CPT theorem, a pillar of quantum field theory, which requires that any Lorentz-invariant local quantum theory is invariant under the combined CPT transformation. In practical terms, a process involving a particle going forward in time is indistinguishable from one involving the antiparticle under time reversal (accompanied by flipping spatial parity and charge) .

Because Feynman diagrams so neatly capture this idea, physicists routinely say things like “an antiparticle is a particle going backward in time” when discussing diagrams . For example, the propagator (quantum amplitude for a particle to travel from point A to B) for an electron with negative energy going backward in time is the same as that of a positron with positive energy going forward . This correspondence has been explicitly verified in countless QED calculations (Bjorken & Drell, 1964). The time-reversible framework of Feynman diagrams also implies certain parity between past and future: if one were to film a particle interaction and run the film backward, one would essentially see a valid particle interaction (with antiparticles and particles exchanged). Indeed, for many reactions, the reversed sequence is physically allowed. A classic example is pair production versus annihilation: an electron and positron can annihilate into photons, and conversely a high-energy photon can produce an electron–positron pair. These are temporal inverses of one another and are related by time-reversal symmetry in the theory. Quantum field theory textbooks emphasize that this formal time-reversibility must be handled carefully. The time reversal operator in quantum mechanics is an anti-unitary operator that not only reverses the time parameter but also flips the momentum and spin directions (Sakurai, 1994). When applied to a multi-particle state, it converts particles to antiparticles (to satisfy CPT invariance) and vice versa. The outcome is that a physically allowed process maps to another allowed process. For example, under time reversal a scattering process |initial ⟶ final⟩ becomes |time-reversed final ⟶ time-reversed initial⟩, which corresponds to all particles replaced by their antiparticles moving oppositely in time. As long as CPT symmetry holds (which experiments thus far uphold to high precision), the microscopic laws are invariant under such transformations. This explains why antiparticles fit seamlessly into relativistic quantum mechanics – their existence is required for consistency with both relativity and time-reversal symmetry (Lüders, 1954).

It should be noted that introducing negative time at the level of Feynman diagrams does not introduce paradoxes because one cannot arbitrarily choose to make one particle go back in time while others do not. The whole diagram – representing a closed interaction history – respects causality overall. Internal lines in diagrams (virtual particles) can be thought of as zig-zagging in time, but they are not directly observable; they are a calculation tool. Observable external particles always have well-defined forward time evolution from the perspective of an experiment. Furthermore, any apparent backward-in-time propagation is constrained by quantum uncertainty and the fact that it occurs only within the interaction region (for instance, within the range of forces). Therefore, even though the calculation might involve negative time intervals, the measurable predictions (cross sections, lifetimes, etc.) come out in agreement with a universe where signals never propagate outside the light cone or back to their origin time. In summary, Feynman diagrams provide a time-symmetric visualization of quantum processes, incorporating the idea of negative time in a way that is fully consistent with quantum mechanics. This visual and mathematical framework underscores how antiparticles can be treated on the same footing as particles by simply reversing time in the diagrams . It also serves as a prelude to more speculative ideas where causes and effects might not be strictly ordered in time, as we explore next in the context of retrocausality and time-symmetric interpretations of quantum theory.

Retrocausality and Time-Symmetric Quantum Interpretations

The success of Feynman’s time-symmetric approach in particle physics encourages one to ask: could retrocausality – influences that go backward in time – play a role in quantum mechanics more broadly? A number of interpretations of quantum theory have been developed that feature explicit time-symmetry, treating the future on an equal footing with the past. These interpretations often aim to resolve or reinterpret quantum paradoxes (such as the measurement problem or the EPR paradox) by allowing what are essentially backward-in-time effects that do not violate causality when properly analyzed. One class of such interpretations posits that the usual forward-evolving quantum state is not the whole story; instead, there may also be a backward-evolving quantum state conveying information from the future.

A pioneering idea in this vein was the Wheeler–Feynman absorber theory in classical electrodynamics, which, while not a quantum interpretation per se, set the stage for time-symmetric thinking. In 1945, John Wheeler and Richard Feynman revisited the question of why an accelerating charge radiates energy. They formulated a theory in which electromagnetic radiation is described by a combination of half-retarded (forward-in-time) and half-advanced (backward-in-time) waves . In their absorber theory, an emitter sends out a field that propagates both forward and backward in time; the presence of absorbers in the future ensures that the advanced components exactly cancel except back at the source, producing the effect of radiation damping at the time of emission . Crucially, the advanced waves traveling toward the past are an integral part of the mechanism: the future absorber’s response travels back in time to meet the emitter at the moment of emission, thereby completing a consistent handshake (Wheeler & Feynman, 1945) . The overall interaction is completely time-symmetric (invariant if $t$ is replaced by $-t$) . No arrow of time is built into the fundamental laws of this theory; the observed arrow (that we see charges emit radiation and not absorb advanced waves from the future) is attributed to the initial/boundary conditions of the universe – essentially, an absence of advanced waves coming in from the infinite future, perhaps due to cosmological conditions or the thermodynamic arrow . The Wheeler–Feynman theory removed the need for self-interaction of charges and eliminated the divergence issues in classical electrodynamics by this clever time-symmetric formulation . While absorber theory itself did not become the standard formulation (fields proved more convenient for most purposes), it deeply influenced later quantum ideas. It demonstrated a case in which allowing backward-in-time effects led to a cleaner, more elegant theory without causing logical inconsistencies . This “handshaking” notion – that a complete interaction might involve a four-dimensional, time-symmetric agreement between future and past – would resurface in quantum interpretations.

One direct progeny of Wheeler–Feynman’s idea in the quantum domain is John Cramer’s Transactional Interpretation (TI) of quantum mechanics. First proposed in 1986, TI explicitly uses both advanced and retarded waves to explain quantum processes (Cramer, 1986). In TI, a quantum emitter sends out an “offer wave” (the usual Schrödinger wavefunction, traveling forward in time) to potential absorbers . When an absorber receives this wave, it generates a response signal – a “confirmation wave” – that travels backward in time to the emitter . The emitter and absorber then effectively negotiate, and a transaction is formed when the offer and confirmation waves align consistently. This transaction is a quantum handshake that spans time: it begins at the emitter and ends at the absorber, but it is all one holistic quantum event encompassing both emission and absorption with equal status. Through this atemporal handshake, energy, momentum, and other conserved quantities are transferred, and the probabilities of different outcomes can be calculated. The wavefunction collapse in TI is not a mysterious instantaneous action but rather the completion of a transaction, which is a process outside time – it does not occur at a single moment but involves the absorber’s future confirming the emitter’s past . By construction, TI is explicitly time-symmetric and avoids the measurement paradoxes of Copenhagen interpretation, while also being non-local (the handshake can connect spacelike-separated events) yet consistent with relativity because the advanced and retarded effects combine in a way that prevents usable faster-than-light signals (Cramer, 1986; Cramer, 1988). In Cramer’s words, the transactional interpretation “permits quantum-mechanical wave functions to be interpreted as real waves physically present in space” – with one set moving forward and another backward in time – and it “resolves various quantum paradoxes” by eliminating the need for a single observer-induced collapse . TI can give intuitive accounts of perplexing experiments like the double-slit experiment and the delayed-choice quantum eraser by invoking handshake correlations that link the experimental configuration in the future with the particle behavior in the past, without any violation of causality. For instance, in a Wheeler’s delayed-choice scenario (Wheeler, 1978) – where the method of detection (interference vs. particle-like) is decided after a photon passes through slits – TI would say the photon’s offer wave went through both slits, and the later choice of detector sent confirmation waves backward to inform how the transaction would form, thus the photon’s history is decided consistently with the future measurement setting. This sounds retrocausal, and indeed it is; but because it respects the rule that only confirmed transactions (which appear as normal outcomes) occur, no observer can use this to signal backwards in time. Numerous quantum paradoxes, from Schrödinger’s cat to the “quantum liar paradox” (Kastner, 2012), have been analyzed under TI, and it remains an active interpretation in the literature.

Another approach embracing time symmetry is the two-state vector formalism (TSVF) developed by Yakir Aharonov and colleagues. TSVF posits that a quantum system at a given time is fully described not only by the usual wavefunction evolving from past to future, but also by a backward-evolving state coming from the future back to the past. In the original 1964 paper by Aharonov, Bergmann, and Lebowitz, they showed that if one pre-selects an initial state and post-selects a final state, one can construct a two-state description that is completely symmetric in time (Aharonov et al., 1964) . The forward-evolving state (propagating per Schrödinger’s equation) and the backward-evolving state (propagating from the final boundary condition) together provide a richer description of intermediate measurements. This leads to well-known results such as the ABL rule for intermediate measurement probabilities and the idea of weak measurements that reveal the so-called “weak values,” which can sometimes lie outside the range of eigenvalues (Aharonov et al., 1988). In TSVF, the two state vectors (one from the past, one from the future) jointly determine the behavior of the system at intermediate times. This is a kind of retrocausality because the future boundary condition (for example, post-selecting on a certain final state) can affect outcomes in the past (between preparation and final measurement). Yet, like other time-symmetric interpretations, TSVF yields no practical inconsistency – it is empirically equivalent to standard quantum mechanics and cannot be used to send messages to the past (it respects linearity and no-signaling). Proponents of TSVF argue that it provides a more complete description of reality, where quantum events are seen as “determined by both initial and final conditions” rather than the past alone (Aharonov & Vaidman, 1991) . This challenges the usual causal narrative but in a way that might soften the measurement problem: probabilities can be viewed as arising from interference of forwards and backwards evolving amplitudes. The time-symmetric reformulation also illuminates certain symmetries and conservation laws. For instance, in situations with particular symmetry, one can derive that any time-symmetric ontology (treating past and future equivalently) must imply retrocausality unless trivial (Price, 2012). As philosopher-physicist Huw Price has argued, if quantum phenomena are fundamentally time-symmetric, then requiring an explanation of EPR-type correlations that does not allow any action-at-a-distance likely forces us to admit influences that act backwards in time (Price, 1996). In other words, retrocausality might be the “price” of eliminating spooky action while keeping Lorentz invariance (Price & Wharton, 2015). This line of thought has motivated researchers to develop explicit retrocausal models that can account for quantum correlations without violating relativistic causality (Wharton, Miller, & Price, 2011 ; Evans et al., 2020). Indeed, recent work reformulating Bell’s theorem has shown that if one allows the hidden variables in a quantum model to depend on future measurement settings (a mild form of retrocausality), one can bypass some of Bell’s constraints and potentially have a locally mediated explanation of entanglement . These models remain speculative, but they demonstrate that the idea of negative time (retrocausal influence) is taken seriously as a solution to deep problems in quantum theory.

Historically, one of the earliest proposals of quantum retrocausality came from Olivier Costa de Beauregard, a student of de Broglie. In 1953, just after the famous EPR paradox paper and Bohm’s spin version of it, Costa de Beauregard suggested that the two particles in the EPR scenario could remain correlated by means of a “succession of advanced and retarded waves” – essentially, one particle’s measurement sends an influence backward in time to the common origin, and then forward in time to affect the other particle . This was a zigzag causal chain through spacetime, fully within the light cone in each segment, yet resulting in the nonlocal correlation at detection . By this mechanism, EPR’s “spooky action at a distance” could be eliminated in favor of more palatable (if non-intuitive) local but retrocausal effects. At the time, even de Broglie found this idea too radical and discouraged its publication . It wasn’t until much later, after Bell’s theorem (Bell, 1964) and its experimental verification (Aspect et al., 1982) , that physicists and philosophers revisited such ideas. Today, retrocausal interpretations form an active subfield in the foundations of quantum mechanics (see Stanford Encyclopedia of Philosophy: “Retrocausality in Quantum Mechanics” for an overview ). While no retrocausal interpretation has been definitively proven as the “correct” one, they provide fertile ground for resolving apparent conflicts between quantum mechanics and relativity. By positing a more nuanced role for time, these interpretations can often explain quantum paradoxes without invoking mysterious instantaneity or parallel universes. They do, however, come at the cost of accepting that the future can subtly influence the present – a notion that challenges our everyday understanding of causation.

Importantly, even in retrocausal interpretations, we do not encounter uncontrolled paradoxes. The scenarios are constructed so that any causal loops are self-consistent (much like the “Novikov self-consistency principle” in time-travel hypotheses (Novikov, 1983)). In quantum retrocausality, one typically finds that retrocausal effects cannot be exploited to send information to the past and create contradictions – the universe finds a way to enforce consistency, often through quantum uncertainty or statistical outcomes. For example, in the transactional interpretation, if one were to attempt a paradoxical situation (such as making a choice that would seem to invalidate a past event), the result would simply be that no transaction forms – the attempt fails rather than leading to inconsistency. Similarly, in two-state vector experiments, one can never retrodict a single outcome with certainty unless it was already determined by the final boundary condition; one cannot “change” the past, one can only infer that certain future conditions correlate with certain past conditions (Griffiths, 2012). Thus, the paradoxical nature of negative time is tamed in these interpretations by quantum laws themselves. Retrocausality in quantum mechanics lives in a delicate balance: it allows the formalism to be symmetric and resolve certain puzzles, but it hides its tracks perfectly when it comes to observable causality – thereby respecting all empirical data we have.

Wheeler–Feynman Absorber Theory and the Quest for Time-Reversal Symmetry

As mentioned, the Wheeler–Feynman absorber theory is a cornerstone in the historical development of time-symmetric physics. It’s worth a closer look both on its own merits and for its influence on later ideas. Wheeler and Feynman (1945) constructed their absorber theory by requiring that the fundamental equations be invariant under time reversal, and by positing that all electromagnetic interactions are mediated through the direct interparticle action of advanced and retarded fields . They built on earlier hypotheses by Tetrode (1922) and others that tried to eliminate free fields in favor of direct particle interactions. In the Wheeler–Feynman picture, when an electron shakes (accelerates), it sends out a field pulse. Half of this pulse is the normal retarded field that goes out to influence other charges in the future; the other half is an advanced field that travels into the past. Now, consider an entire universe of charged particles. The advanced response of the absorber (essentially, all the other charges that will eventually feel the retarded pulse) comes back and meets the emitter precisely at the moment of emission . The result is that the emitter experiences a recoil force (radiation reaction) as if it is already feeling the effect of radiating into the rest of the universe. Meanwhile, the net field observed in normal history (for $t$ after emission) is just the retarded field – the advanced fields cancel out everywhere except at the source. This cleverly explains radiation without self-interaction and without advanced effects in our observed timeline, yet the law of interaction itself is time-symmetric . The “arrow” of radiation (that we see electromagnetic waves emanating from sources rather than coming in) is explained by a kind of boundary condition: the universe has abundant charges to act as absorbers in the future but presumably not a mirroring set of charges in the infinite past sending advanced waves (or if it did, we would have to include them too). In their later work, Wheeler and Feynman discussed how the thermodynamic arrow of time might select the retarded solution in practice . If, for example, the universe had a “temporal asymmetry” such as a big bang with initially low entropy, one could get an imbalance between advanced and retarded influences that yields the effective one-way flow we observe (Hoyle & Narlikar, 1995) . In any case, absorber theory showed concretely that it’s possible to have a well-defined physical theory where negative-time propagation (advanced waves) is not only allowed but essential, and yet no contradictions arise and the ordinary cause-effect chronology emerges for macroscopic phenomena.

The absorber idea was later extended by Fred Hoyle and Jayant Narlikar in the 1960s and 1990s, who tried to apply it to gravity and cosmology. Hoyle and Narlikar developed a fully time-symmetric electrodynamics and gravitation theory in which the arrow of time is tied to the expansion of the universe (cosmological absorber condition) . Their work, while not part of mainstream cosmology, further cemented the understanding that time-symmetric laws are viable and that the initial or boundary conditions (like an expanding universe with a certain matter distribution) are what breaks the symmetry and yields an arrow (Hoyle & Narlikar, 1964; Hoyle & Narlikar, 1995) . In these models, if the universe were different (say, contracting towards a big crunch with a future absorber rather than a past one), one could in principle see the opposite arrow. This reinforces a philosophical point: time’s arrow may not be a fundamental law, but rather a contingent fact about the state of our universe (Price, 1997). The microscopic equations could permit negative time (time reversal) solutions freely, and only a cosmological asymmetry (and the resultant growth of entropy as per the Second Law of Thermodynamics) prevents us from routinely seeing advanced effects. Indeed, experiments in highly controlled settings can sometimes isolate nearly time-symmetric behavior – for example, spin echo experiments in NMR can reverse the dephasing of spins, effectively “rewinding” a quantum system for a short time, highlighting that no fundamental law prevents such reversal (Hahn, 1950).

The Wheeler–Feynman theory itself has not been experimentally proven or disproven in a direct sense, because standard electrodynamics (with only retarded fields) makes the same predictions for observable quantities in normal conditions. However, its legacy is evident: it inspired Cramer’s transactional interpretation, as Cramer explicitly “revived the Wheeler–Feynman idea of two waves” for quantum processes . It also gave confidence to those exploring hidden-variable theories that perhaps one could use both forward and backward evolving solutions to construct deterministic accounts of quantum phenomena (as in some attempts by Davies and Pegg in the 1970s, or the more recent causally symmetric Bohmian mechanics developed by Roderick Sutherland (2008) where the guiding equation is influenced by both past and future boundary conditions) . All these are threads in the tapestry of physicists grappling with the implications of negative time. In each case, the common strategy is to double the description – include both a forward-time and a backward-time component – in such a way that they fit together consistently and reproduce the observed reality where phenomena predominantly follow the forward arrow. Wheeler and Feynman’s work taught us that consistency is possible and even elegant.

Experimental Considerations and Time-Reversal Symmetry

Finally, we turn to the experimental status of time-reversal symmetry and related considerations. Are the fundamental laws of physics invariant if we substitute $t$ with $-t$? For the most part, yes – except in scenarios involving the weak nuclear force. It has been known since 1964 that processes governed by the weak interaction can violate combined charge-conjugation and parity symmetry (CP violation), as discovered in neutral kaon decays (Christenson et al., 1964) . By the CPT theorem, any CP violation in a Lorentz-invariant local theory implies a corresponding violation of time-reversal (T) symmetry. For many years, this T-violation was inferred indirectly from CP-violation experiments assuming CPT invariance. In 2012, however, a direct observation of T symmetry violation was achieved by the BABAR experiment with B mesons (Lees et al., 2012) . By comparing the probabilities of certain B meson transitions and their time-reversed counterparts (using entangled B–anti-B pairs to provide an initial vs. final state swap), BABAR observed a clear difference, providing unambiguous evidence that the microscopic physics is not invariant under time reversal . Similarly, an earlier experiment at CERN, CPLEAR (Angelopoulos et al., 1998), directly measured time-reversal noninvariance in the neutral kaon system by observing asymmetries in $K^0 \rightarrow \bar K^0$ transitions versus the reverse . These results confirm that nature itself exhibits a slight preference for one direction of time in the realm of subatomic decays – a preference linked to the matter–antimatter asymmetry in the universe (Sakharov, 1967). It’s important to note, however, that these violations of T-symmetry are very specific. They occur in rare decay processes and involve complex phases in the weak interaction Lagrangian. In contrast, the electromagnetic and strong interactions have been tested and found to respect T symmetry extremely well. For example, no electric dipole moment (EDM) of the neutron or electron has been found at current sensitivities, and such an EDM would signal T (and P) violation in electromagnetic interactions. The absence of an EDM imposes strict limits on any time-reversal violation in QED or QCD . Therefore, aside from the peculiar case of weak decays, all known phenomena are T-symmetric when viewed at the fundamental level. If we were to reverse the motion of planets, the flow of photons, or the interactions of electrons and protons (and also flip spins and magnetic fields appropriately), the equations of motion (Newton’s, Maxwell’s, Schrödinger’s, etc.) would still hold true. This underlying time symmetry is what allows the theoretical constructs discussed earlier (antiparticles as reversed-time particles, time-symmetric quantum interpretations) to be plausible.

On the other hand, thermodynamics and quantum measurement introduce asymmetry. An isolated system might have time-symmetric equations, but when you have many degrees of freedom and entropy, reversing time becomes practically impossible. A movie of two entangled particles creating correlated outcomes looks just as plausible in reverse (it would show two particles becoming entangled via some interaction – which can indeed happen). But a movie of eggs unscrambling or a Geiger counter “un-clicking” looks absurd in reverse because those involve thermodynamic irreversibility. Measurement amplifies quantum effects to the macroscopic scale, entangling the quantum system with a large environment (the measuring device, air molecules, etc.), thereby entangling with an effectively irreversible increase in entropy. This is why, although the microphysics might permit negative-time descriptions, we don’t encounter macroscopic paradoxes – any attempt to observe something like an advanced wave directly is swamped by the many irreversible processes accompanying our observation. Nonetheless, experiments can cleverly test the edge of time symmetry. “Loschmidt echo” or time-reversal echo experiments in quantum systems have been performed, where a system’s Hamiltonian is reversed after some evolution, leading to a partial return to the initial state (Peres, 1984). These experiments confirm that to the extent we can isolate a system and control its dynamics, the evolution is indeed reversible (apart from decoherence). In NMR, the spin echo technique is a prime example: by flipping spins at the right time, one can reverse dephasing and get a refocused signal, effectively undoing the intermediate evolution. Such demonstrations underline that quantum mechanics has no built-in arrow of time – the arrow emerges from initial conditions and macroscopic irreversibility, not from the microscopic laws.

Another line of experiments relevant to negative time are the delayed-choice and quantum eraser experiments, which bear on the question: can future choices affect past events in quantum mechanics? In John Wheeler’s classic delayed-choice thought experiment, one decides whether to observe a photon’s interference pattern or particle path after it has already passed through a double-slit apparatus. Quantum mechanics predicts (and experiments confirm (Kim et al., 2000) ) that the photon’s behavior is consistent with whichever measurement is eventually made – as if the photon “knew” the experimental setup even after it went through the slits. This retroactive consistency is often described in headlines as the “future affecting the past,” but in standard quantum theory no signal or causal influence is traveling backward; instead, the phenomenon is explained by the photon not having determined its behavior until the measurement (the choice of measurement alters the waveform globally, but not in a way that can send information backward). However, interpretations like the transactional interpretation or two-state vector formalism provide an intuitive retrocausal narrative for these results: the future measurement apparatus sends a confirmation wave or backward-evolving state that merges with the forward-evolving state, resulting in a transaction or consistent history. The outcomes are exactly as quantum mechanics predicts, but the interpretation can be time-symmetric. Similarly, quantum eraser experiments (Scully & Drühl, 1982; Walborn et al., 2002) show that “erasing” which-path information after the fact can restore interference that was seemingly lost – again suggesting a kind of retroactive change. Yet careful analysis shows no causality violation: one cannot erase information in a way that is known to an observer before the interference is measured; when one looks at the total pattern without conditioning on the erasure, it contains no interference. Only by correlating with the later erasure choice (which does not reach the earlier detector in any direct causal sense) does one see the interference in subsets of the data. So, quantum mechanics respects causality, but it also allows these intriguingly consistent retro-patterns that invite a time-symmetric storytelling.

In terms of fundamental symmetries, ongoing experimental efforts continue to probe time-reversal invariance. Searches for electric dipole moments (EDMs) of neutrons, electrons, atoms, and molecules are effectively searches for T-violation (assuming CPT). The latest neutron EDM experiments (Abel et al., 2020) push the bounds lower and lower, because a nonzero EDM would indicate a permanent T-asymmetry in the particle’s properties. So far, no EDM has been seen, which constrains theories of beyond-the-Standard-Model physics (many of which predict additional T-violating processes). Meanwhile, in the realm of neutrinos, there is ongoing investigation of CP violation which by CPT would imply T violation – though neutrino oscillation experiments have hints of CP asymmetry, it’s not yet clear. The upshot is that except for the peculiar K and B meson systems, time-reversal symmetry appears to hold in all subatomic processes we’ve examined. This is good news for the consistency of physics: it means we can reliably use time-symmetric equations in our theories and interpretations without fear of contradicting experiments (so long as we account for the known T-violations in the weak interaction through appropriate terms).

Conclusion:

Negative time – the notion of processes evolving backward in time – occupies a fascinating and nuanced position in quantum physics. On the one hand, our everyday experience and thermodynamic commonsense tell us that cause precedes effect and that the past is fixed while the future is open. On the other hand, the fundamental equations of quantum theory (and relativity) are largely time-symmetric, allowing temporal reversals and negative-time trajectories as valid mathematical solutions. Quantum physics has turned what seems like a paradox into a powerful tool: by interpreting negative time solutions as antiparticles, Feynman and Stueckelberg showed that one could elegantly account for antimatter within the same formalism as matter . This insight removed a major conceptual barrier and yielded calculations that matched experiments to stunning accuracy. Far from causing logical inconsistencies, the allowance for “backward in time” descriptions in quantum field theory has been a triumph, embodied in the widely used Feynman diagrams that implicitly sum over all possible time orderings (including negative-time propagations) while ultimately predicting positive-time observable outcomes.

Moreover, negative time appears as a central ingredient in several interpretations of quantum mechanics that strive for deeper understanding of quantum nonlocality and the measurement process. Time-symmetric interpretations like the transactional interpretation and two-state vector formalism embrace retrocausality at a conceptual level, hypothesizing that nature might be better described as a handshake between past and future, or by quantum states defined by two time-boundary conditions (initial and final) rather than one. These frameworks provide intuitive (if unconventional) ways to understand phenomena that are puzzling in a purely forward-causal picture, such as how a particle’s behavior can seemingly adjust to a future experimental setup (delayed-choice experiments) or how entangled particles coordinate their outcomes instantly. By allowing influences to propagate backward in time (in a carefully restricted manner), the interpretations achieve a form of locality or realism that is otherwise hard to come by in quantum foundations . Crucially, all well-constructed retrocausal models thus far respect the principle of “no paradoxes, no free lunch.” They do not let us build a time machine or send a message to our younger selves. Instead, they reveal a picture of the quantum world in which the strict ordering of cause and effect can blur at the micro level – yet when all is said and done, the accounting is consistent and our classical experience emerges intact.

From the Wheeler–Feynman absorber theory in the 1940s to modern investigations of entanglement and quantum information, the exploration of time-symmetric and retrocausal ideas has greatly enriched our understanding. It has taught us that many supposed constraints (e.g. “causes must always precede effects”) are not built into the fundamental laws but are emergent features of the solutions we, by habit or by boundary conditions, choose to focus on. Negative time solutions are not only mathematically acceptable; they are physically meaningful when interpreted with care. They remind us that nature’s true laws might be symmetric and elegant, and what we call the arrow of time may arise from asymmetries in initial conditions or specific interactions (like the weak force) rather than the core equations. Indeed, the confirmed existence of T-violation in weak decays provides a concrete example where the arrow of time enters at the micro level, offering clues (through Sakharov’s conditions) to the dominance of matter over antimatter in the universe. Here, the interplay of symmetry and asymmetry is on display: the laws allow time-reversed processes, but a slight excess of one process over its reverse (CP/T violation) combined with cosmic initial conditions helped shape the universe’s evolution.

In conclusion, investigating negative time in quantum physics reveals a world where time is not always a one-way street. Instead, time can be a two-way medium in the quantum realm, with particles and waves exploring multiple temporal directions in calculations and interpretations. The implications are profound: they touch on the nature of causality, the interpretation of quantum theory, and even the origin of the arrow of time itself. Yet, through all these explorations, quantum physics has maintained logical consistency and agreement with experiment. The paradoxes that negative time seems to threaten us with have found resolutions within the quantum framework. Whether through the reinterpretation of antiparticles, the atemporal coherence of a transaction, or the self-consistency of a two-state description, physicists have found ways to fit negative time into a positive theory. Far from science fiction, the role of negative time in quantum mechanics is grounded in rigorous mathematics and empirical support. It challenges our classical intuitions but in doing so opens the door to a more complete understanding of the temporal symmetry underlying physical law. Future research – in fields ranging from quantum gravity (where time symmetry might be fundamental) to quantum computing (where time-reversal operations are used in error correction and algorithmic reversals) – will continue to probe the boundaries between past and future. The lessons learned from the concept of negative time will undoubtedly play a guiding role in these endeavors, reminding us that time in quantum physics is perhaps best viewed not as an absolute arrow, but as a dimension in which surprising, yet logically consistent, twists are possible.

References

Abel, C., et al. (2020). Measurement of the permanent electric dipole moment of the neutron. Physical Review Letters, 124(8), 081803.

Aharonov, Y., Bergmann, P. G., & Lebowitz, J. L. (1964). Time symmetry in the quantum process of measurement. Physical Review, 134(6B), B1410–B1416 .

Aharonov, Y., & Vaidman, L. (1991). Complete description of a quantum system at a given time. Journal of Physics A, 24(10), 2315–2328 .

Aharonov, Y., & Vaidman, L. (2007). The two-state vector formalism: An updated review. In J. G. Muga, R. Sala Mayato, & Í. L. Egusquiza (Eds.), Time in Quantum Mechanics (Lecture Notes in Physics 734, pp. 399–447). Springer .

Aharonov, Y., & Tollaksen, J. (2010). New insights on time-symmetry in quantum mechanics. Physics Today, 63(11), 33–38.

Almada, L., Ch’ng, K., Kintner, S., Morrison, B., & Wharton, K. B. (2016). Are retrocausal accounts of entanglement unnaturally fine-tuned? International Journal of Quantum Foundations, 2(1), 1–16.

Anderson, C. D. (1933). The positive electron. Physical Review, 43(6), 491–494.

Angelopoulos, A., et al. (CPLEAR Collaboration) (1998). First direct observation of time-reversal non-invariance in the neutral kaon system. Physics Letters B, 444(1–2), 43–51 .

Aspect, A., Dalibard, J., & Roger, G. (1982). Experimental test of Bell’s inequalities using time-varying analyzers. Physical Review Letters, 49(25), 1804–1807 .

Bell, J. S. (1964). On the Einstein Podolsky Rosen paradox. Physics, 1(3), 195–200.

Bjorken, J. D., & Drell, S. D. (1964). Relativistic Quantum Mechanics. McGraw-Hill.

Boh, D. (1952). A suggested interpretation of the quantum theory in terms of “hidden” variables I and II. Physical Review, 85(2), 166–193.

Christenson, J. H., Cronin, J. W., Fitch, V. L., & Turlay, R. (1964). Evidence for the 2π decay of the $K_2^0$ meson. Physical Review Letters, 13(4), 138–140 .

Costa de Beauregard, O. (1953). Commentaires à l’article d’Einstein, Podolsky et Rosen. Comptes Rendus de l’Académie des Sciences, 236, 1632–1634 .

Costa de Beauregard, O. (1977). Time symmetry and the Einstein paradox. Il Nuovo Cimento B, 42(1), 41–64.

Cramer, J. G. (1986). The transactional interpretation of quantum mechanics. Reviews of Modern Physics, 58(3), 647–687 .

Cramer, J. G. (1988). An overview of the transactional interpretation of quantum mechanics. International Journal of Theoretical Physics, 27(2), 227–236.

Dirac, P. A. M. (1930). A theory of electrons and protons. Philosophical Magazine, 5(30), 321–341.

Dirac, P. A. M. (1931). Quantised singularities in the electromagnetic field. Proceedings of the Royal Society A, 133(821), 60–72.

Einstein, A., Podolsky, B., & Rosen, N. (1935). Can quantum-mechanical description of physical reality be considered complete? Physical Review, 47(10), 777–780.

Feynman, R. P. (1949). The theory of positrons. Physical Review, 76(6), 749–759 .

Feynman, R. P. (1965). The development of the space–time view of quantum electrodynamics. Science, 153(3737), 699–708. (Nobel Lecture, December 1965).

Feynman, R. P., & Hibbs, A. R. (1965). Quantum Mechanics and Path Integrals. McGraw-Hill.

Griffiths, R. B. (2012). Quantum theory: Constraints on retrocausality and definition of a causal vector. Physical Review A, 85(5), 052115.

Hahn, E. L. (1950). Spin echoes. Physical Review, 80(4), 580–594.

Hoyle, F., & Narlikar, J. V. (1964). A new theory of gravitation. Proceedings of the Royal Society A, 282(1389), 191–207 .